Definición
Una sucesión infinita es una función cuyo dominio es el conjunto de los números naturales ordenados como
a1, a2, a3,..., an
Cada uno de los números que componen la sucesión se llama término de la sucesión. Se nombran con una letra y un subíndice que depende del lugar que el término ocupa en la sucesión.
A veces, podemos encontrar una expresión (fórmula) que sirve para obtener un término cualquiera de la sucesión con solo saber el lugar que este ocupa. A esta expresión se le llama término general
Ejemplo: Sucesión
Dada la sucesión
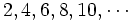
- a) Halla el término 10.
- b) Halla el término general
|
SUCESIONES DEFINIDAS RECURSIVAMENTE
|
|
Los valores de los términos de una sucesión pueden definirse explícitamente mediante fórmulas como
Definición recursiva de sucesión Una sucesión (B)Cláusula base: Los valores de algunos términos de la sucesión, generalmente el primero, o los primeros, se especifiquen explícitamente. (R)Cláusula recursiva: Los valores de los otros elementos de la sucesión están definidos en término de valores previos en la sucesión. En la cláusula base se dan los valores de los elementos a partir de los cuales se generan los demás valores de la sucesión. La cláusula recursiva nos describe la manera (reglas o fórmulas) para obtener los otros valores de la sucesión (de manera “recurrente”). Ejemplo: Sucesiones aritméticas
La sucesión definida por Es un ejemplo de sucesión aritmética, en donde cada término se obtiene del anterior sumándole 2. Una definición recursiva de esta sucesión es:
En general, una sucesión aritmética es una sucesión en la cual cada término después del primero se obtiene sumando al término precedente un mismo número fijo d, llamado diferencia común. Es decir, una sucesión aritmética es de la forma
Teniendo en cuenta la definición anterior, una manera de definir recursivamente una sucesión aritmética con diferencia común d es:
(B)
(R)
Utilizando esta definición para la sucesión aritmética con primer término
|


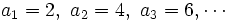 .
. , que en este caso es el 20.
, que en este caso es el 20.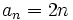 porque cada término se obtiene multiplicando la posición que ocupa por 2.
porque cada término se obtiene multiplicando la posición que ocupa por 2.