Congruencia de triángulos
METAS DE COMPRENSIÓN
Las estudiantes desarrollarán comprensión acerca de:
- Cómo aplicar los criterios de congruencia de triángulos en la solución de problemas.
- Cómo resolver problemas relacionados con congruencia de triángulos, empleando procedimientos hipotético - deductivo y de afirmación - razón.
Marco teórico
La congruencia de triángulos se basa en el estudio de la igualdad entre triángulos, es decir, gracias a esto podemos saber si dos triángulos o más son congruentes (iguales) entre sí. Dicho de modo sencillo, nos permite comparar varios triángulos y saber si son iguales (si tienen los mismos ángulos en sus vértices y si sus lados miden lo mismo).
Entonces, sabemos que si dos triángulos tienen tres ángulos y tres lados iguales entre si, son iguales (o congruentes), ahora bien, no es necesario en todos los casos verificar uno a uno todos esos elementos. Hay veces que con mirar tres pares de elementos nos llega, para ello vamos a utilizar los llamados criterios de congruencia, viendo cada una de las posibilidades por separado:
POSTULADOS DE CONGRUENCIA
1º L-L-L
Considerando dos triángulos de lados A, B y C y D, E y F, se dice que son congruentes, si sus lados son iguales entre sí, es decir:

NOTA: Las letras en mayúscula denotan los vértices, mientras que las minúsculas se refieren a los lados, mas adelante usaremos letras griegas (beta, gamma...) para referirnos a los ángulos, es solo nomenclatura establecida, es decir, es así porque se pusieron de acuerdo entre todos.
2º L-A-L

Considerando los mismos triángulos de lados A, B y C y D, E y F respectivamente, se dice que son congruentes si tienen dos lados iguales y el ángulo que se forma con la unión de estos (en el vértice).
3º A-L-A
Teniendo un lado igual (que mida lo mismo, es decir, que sea congruente), y con los ángulos que se forman en los extremos de dicho lado también congruentes. A estos ángulos se les denomina adyacentes al lado.

4º LLA
Con dos lados iguales (congruentes) y los ángulos opuestos al mayor de los lados también son congruentes.
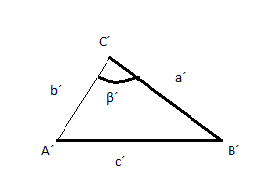
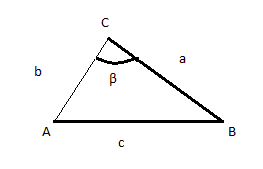
Considerando beta y beta prima ángulo iguales y lo mismo para a y b con sus homónimos a´y b´.
Tomado de:https://matematica.laguia2000.com/general/congruencia-de-triangulos
Ver también
https://tutormatematicas.com/GEO/Triangulos_congruentes_LLL_LAL_ALA_AAL_CC_HC_HA_CA.html


